 |
Gli pneumatici della motocicletta
|
Ha più grip..ha meno grip sul bagnato...sono gomme tenere, medie, no sono gomme dure?.......tutti termini usati frequentemente per definire il comportamento e la qualità degli pneumatici.
Ma cosa vogliono dire? Cosa significa chiedere quanto grip ha? Quanto è tenera o dura la gomma?
Cosa significa definire tenera una gomma?........termini usati più propriamente nel caso delle costate di manzo.
E' come se confrontando diversi motori si dicesse: è più potente o meno potente, ha più coppia o meno coppia, senza conoscere i concetti di coppia e di potenza e senza quindi associare a queste grandezze dei valori numerici espressi in Kw e Nm.

Cerchiamo di fare un pò di chiarezza dando delle risposte a delle semplici e intuitive domande.
Quale è il compito del pneumatico?
La risposta è semplice, il pneumatico deve assolvere due scopi:
- consentire il trasferimento della forza di spinta o di frenata a terra;
- generare la forza laterale necessaria per il mantenimento dell'equilibrio del motociclo in curva, o lungo una traiettoria curvilinea come quelle generate ad esempio per schivare un ostacolo, per effettuare un cambio di corsia o per percorrere una curva ad S.
Cerchiamo ora di capire come si genera la forza laterale e che valore deve avere quando il motociclo percorre una curva a raggio e a velocità costante (regime stazionario) e da quali grandezze dipende.
E' facile intuire che la forza laterale dipende dal carico verticale agente sulla ruota. Maggiore è il carico maggiore è la forza laterale generata. Meno intuitivo è comprendere la dipendenza della forza laterale dall"angolo di rollio (angolo di piega) e dallo strisciamento laterale del pneumatico, strisciamento laterale espresso dall"angolo di deriva che sarà definito nel seguito.
La forza laterale dipende non solo dal carico, dall'angolo di rollio e dall'angolo di deriva ma anche da altri due parametri che i motociclisti conoscono bene: l a pressione di gonfiaggio e la temperatura del pneumatico in condizioni di esercizio.Consideriamo dapprima l'effetto dell'angolo di rollio.
L'impronta del pneumatico in posizione verticale con il piano stradale ha una forma simmetrica ed ellittica; l"impronta rappresentata nella figura 1 è colorata con toni di grigio la cui intensità è proporzionale alla pressione tra ruota e piano stradale.
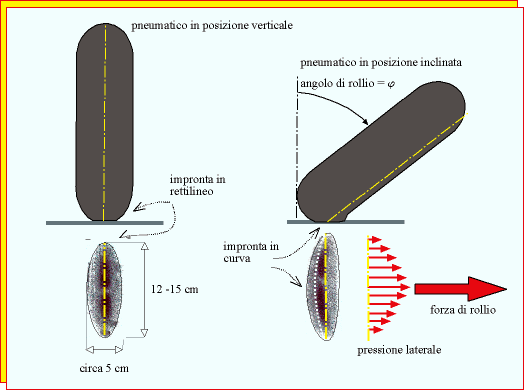
Figura 1. La figura rappresenta l' impronta del pneumatico su piano stradale e rispettivamente in posizione verticale e inclinata. L'intensità del tono di grigio nel disegno dell'impronta è proporzionale alla pressione tra pneumatico e piano stradale.
Come si può osservare nella figura posta a destra, quando la ruota è inclinata, la particella di gomma che percorre l'impronta non segue la traiettoria che seguirebbe se non vi fosse contatto con la strada. E' costretta proprio a causa del contatto con la strada a seguire una traiettoria diversa, ossia il contatto con la strada provoca la deformazione della carcassa del pneumatico, deformazione che dà origine ad una forza laterale crescente all'aumentare dell"angolo di rollio.
Per capire meglio questo effetto si pensi ad un pneumatico indeformabile, come se fosse di metallo, che quindi è a contatto con il piano stradale in una zona piccolissima assimilabile ad un punto. In questo caso non essendoci deformazione della carcassa ed essendo il contatto puntiforme la forza dovuta al rollio risulterebbe nulla.
La forza dovuta al rollio dipende quindi dalla forma e dalle dimensioni dell'impronta, grandezze dell'impronta che dipendono a loro volta dalle caratteristiche geometriche del pneumatico (raggio del pneumatico e raggio della sezione) e dalla rigidezza laterale e radiale della carcassa.
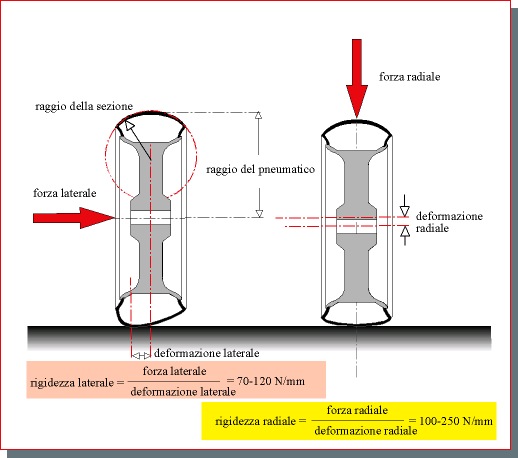
Figura 2. Le rigidezze radiale e laterale dipendono dalle geometria, dal tipo di pneumatico (anteriore o posteriore), dalle caratteristiche costruttive della carcassa (radiale, a tele incrociate), dalla pressione e dal carico verticale.
Consideriamo ora l'effetto dello strisciamento laterale ossia dell' angolo di deriva.
Si definisce angolo di deriva l'angolo tra la direzione della velocità di avanzamento e il piano della ruota. L'impronta in presenza di strisciamento laterale risulta avere una forma asimmetrica. Nella prima parte dell'impronta le particelle di gomma tendono a seguire la direzione della velocità di avanzamento, poiché la velocità di avanzamento non coincide con il piano della ruota le particelle contenute nell'impronta si deformano rispetto alla carcassa del pneumatico. E' questa la zona di adesione dell'impronta. Arrivati ad una certa deformazione le forze elastiche di richiamo dovute alla deformazione della gomma superano le forze di adesione e pertanto le particelle di gomma iniziano a strisciare rispetto al piano stradale. In questo caso si ha una zona dell'impronta detta di strisciamento. L'integrale delle pressioni laterali esteso a tutta l'area dell'impronta dà origine alla forza laterale di deriva.
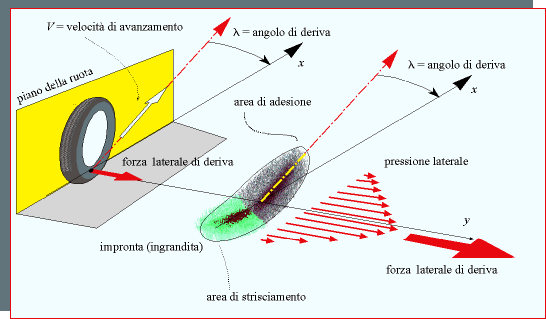
Figura 3. Origine della forza laterale di deriva. La risultante delle pressioni laterali è la forza laterale dovuta all'angolo di deriva.
Abbiamo visto che la forza laterale dipende sia dall'angolo di rollio che dallo strisciamento laterale del pneumatico, strisciamento laterale che abbiamo espresso mediante l'angolo di deriva.
E' consuetudine rappresentare la forza laterale al variare dell'angolo di deriva per valori prefissati dell'angolo di rollio, come rappresentato nella figura 4 nel caso di un pneumatico anteriore di tipo sportivo.
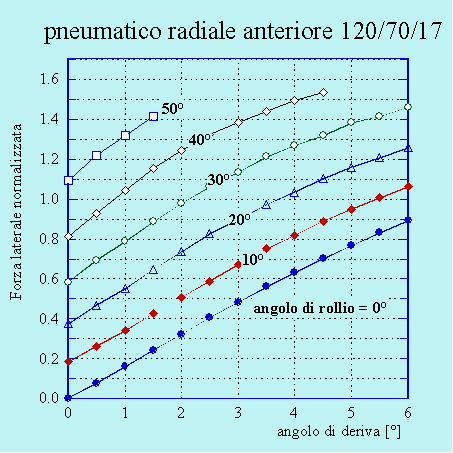
Figura 4. Forza laterale al variare dell'angolo di deriva per vari valori dell'angolo di rollio.
Questo tipo di rappresentazione è usata nel campo automobilistico nel quale ovviamente gli angoli di rollio sono molto piccoli e gli pneumatici producono le forze laterali richieste solo grazie allo strisciamento laterale.
Molto diverso è il caso dei motocicli dove gli pneumatici lavorano principalmente con il rollio e secondariamente con lo strisciamento laterale, almeno per quanto riguarda la produzione della forza laterale. Diventa quindi logico per gli pneumatici motociclistici rappresentare la forza laterale al variare dell'angolo di rollio, per valori discreti dell'angolo di deriva, come rappresentato nella figura 5.
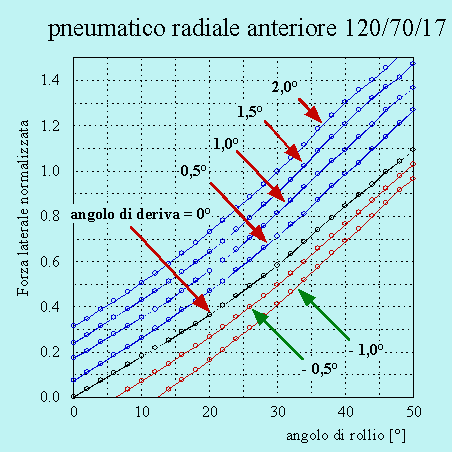
Figura 5. Forza laterale al variare dell'angolo di rollio per vari valori dell'angolo di deriva.
La forza laterale può essere espressa analiticamente mediante una funzione lineare dell'angolo di rollio e dell'angolo di deriva, come se la forza fosse la somma di due componenti indipendenti tra di loro: la componente di rollio e la componente di deriva.
![]()
Le costanti K hanno anche un significato geometrico, rappresentano le tangenti delle curve rispettivamente della forza laterale normalizzata in funzione dell'angolo di rollio, con angolo di deriva nullo, e della forza laterale in funzione dell'angolo di deriva, con angolo di rollio nullo.
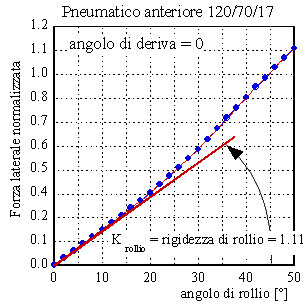
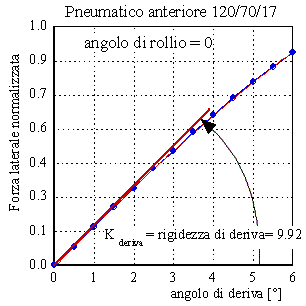
Figura 6. Significato geometrico della rigidezza di rollio e di deriva.Le rigidezze indicate sono espresse in 1/rad.
Per comprendere quanto debba valere la forza laterale consideriamo un motociclo mentre sta percorrendo una traiettoria circolare con raggio costante e a velocità costante.
Se trascuriamo l'effetto giroscopico, generato dalle ruote mentre percorrono la curva, e il fatto che gli pneumatici hanno una sezione considerevole ( il cui raggio medio di curvatura può superare anche i 100 mm nel caso delle ruote posteriori) la forza laterale necessaria per garantire l'equilibrio risulta uguale al prodotto del carico verticale per la tangente dell'angolo di rollio.
![]()
Le ipotesi semplificative introdotte equivalgono a considerare un motociclo virtuale con ruote aventi momento di inerzia molto piccolo (ruote in magnesio o in fibra di carbonio) con sezione molto piccola, tipo le ruote tubolari delle biciclette da corsa.
Ad esempio con un angolo di rollio uguale a 45° la forza laterale è uguale esattamente al carico verticale. La condizione di equilibrio è rappresentata nella figura 6 che mostra che la forza centrifuga viene equilibrata esattamente dalla somma delle due forze laterali generate dai due pneumatici.
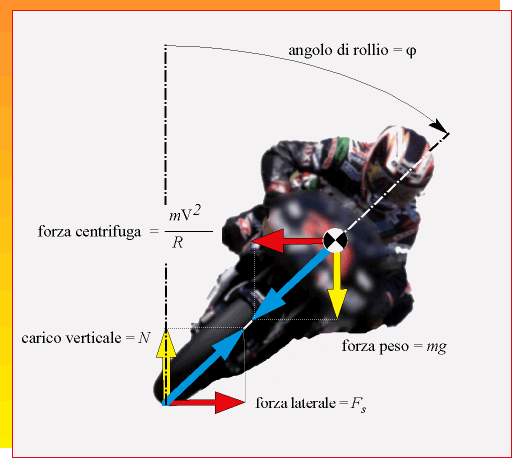
Figura 7. Equilibrio del motociclo in curva. R indica il raggio di curvatura della curva, m la massa del veicolo comprensivo del pilota e V la velocità di avanzamento.
La figura 8 mostra le forze laterali anteriore e posteriore di due pneumatici, rapportate ai rispettivi carichi verticali, al variare dell'angolo di rollio. La figura riporta anche l'andamento della funzione:
![]()
che rappresenta la condizione di equilibrio in curva.
La forza laterale generata dal rollio, rapportata al carico verticale, può risultare inferiore o superiore alla forza richiesta nella condizione di equilibrio rappresentata dal valore della tangente dell'angolo di rollio.
Nel primo caso, con forza di rollio insufficiente, si dovrà avere uno strisciamento laterale ossia un angolo di deriva positivo che produrrà l'aliquota della forza mancante all'equilibrio; nel secondo caso invece l'angolo di deriva dovrà essere negativo in modo da ridurre la forza laterale che per effetto del solo rollio risulta superiore a quella richiesta nelle condizioni di equilibrio.
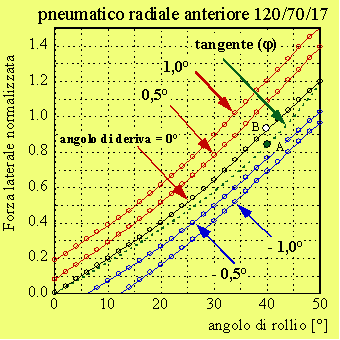
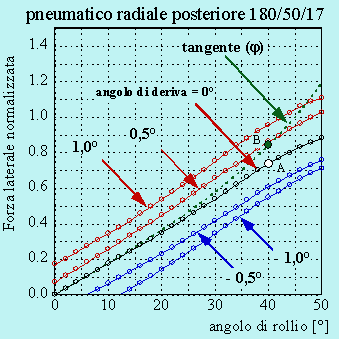
Figura 8. Esempio di forze laterali anteriore e posteriore al variare dell'angolo di rollio. Le curve tratteggiate rappresentano le forze laterali richieste per l'equilibrio in curva.
Consideriamo gli pneumatici le cui caratteristiche sono rappresentate nella figura 7. Supponiamo che il veicolo stia percorrendo una curva e che sia inclinato di 40°. La forza di rollio nel caso del pneumatico posteriore risulta insufficiente per l'equilibrio. Infatti con deriva zero la forza laterale risulta pari a circa 0.73 (punto A) mentre la forza richiesta risulta pari a 0.85. Il pneumatico posteriore quindi striscerà lateralmente verso l'esterno e il valore dell'angolo di deriva sarà proprio tale da far crescere la forza laterale al valore necessario per l'equilibrio, rappresentato dal punto B.
Nel caso del pneumatico anteriore si avrà invece nella condizione di equilibrio un angolo di deriva negativo in quanto, per un angolo di rollio di 40°, la forza prodotta dal solo rollio risulta (punto B) maggiore di quella necessaria per l'equilibrio (punto A).
In questo caso il motociclo, a causa delle caratteristiche degli pneumatici presenta un comportamento sovrasterzante. Infatti se consideriamo la stessa motocicletta che percorre la stessa curva ma equipaggiata con pneumatici ideali, in grado di fornire una forza di rollio proprio uguale a quella richiesta, il raggio di curvatura risulterebbe maggiore come illustrato nella figura 8.
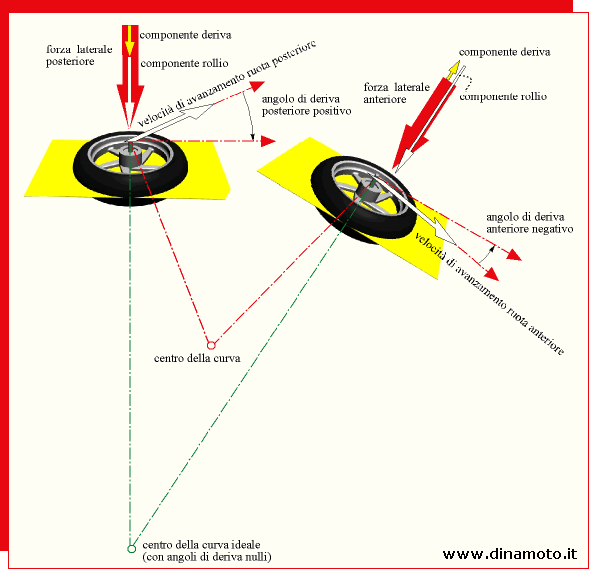
Figura 8. Motociclo in curva visto dall'alto.
Si potrebbe anche montare sull'anteriore un pneumatico scadente e uno prestante sul posteriore. In sostanza si potrebbe avere il caso di pneumatico con deriva al anteriore elevata e con deriva nulla o leggermente negativa al posteriore. Il motociclo presenterebbe con questi pneumatici un comportamento molto sottosterzante. Il comportamento sottosterzante potrebbe risultare pericoloso in quanto, nel caso fosse necessario restringere la curva, si richiederebbe al pneumatico anteriore una maggiore forza laterale ossia in definitiva un maggiore angolo di deriva.
E se il pneumatico non fosse in grado di generare questa maggiore forza cosa succederebbe?
L'anteriore scivolerebbe e la caduta sarebbe certa.
Il problema delle gomme non è tutto qui,
Ad esempio come è la dipendenza della forza di rollio e di deriva dalla temperatura, dalla pressione?
Le forze dipendono dai carichi verticali, in modo proporzionale o non proporzionale?.
Come si combina la forza laterale quando è richiesta una forza longitudinale di frenata o di spinta?
Perchè cambiando gli pneumatici, pur dando una sensazione di tenuta, la guida si sente diversa?
Come vengono influenzate le caratteristiche di maneggevolezza del motociclo dalle caratteristiche degli pneumatici?
Calma, le domande sono molte, a queste domande si cercherà di dare risposte scientifiche corrette nei prossimi articoli.
Nel frattempo incominciamo a chiedere ai costruttori di pneumatici i certificati di collaudo con l'indicazione dei valori delle forze generate al variare dell'angolo di rollio e dell'angolo di deriva, della pressione e della temperatura..
Forse è bene parlare con numeri alla mano........gomma tenera, dura, più grip.......sono solo parole vuote.
